We introduce a general principle for studying the Hausdorff measure of limsup sets. A consequence of this principle is the well-known Mass Transference Principle of Beresnevich and Velani (2006). https://arxiv.org/pdf/1808.02135.pdf
The main result is as follows.
\begin{theorem}[Hussain-Simmons, 2018]\label{HS:thm}
Fix ![]() , let
, let ![]() be a sequence of open sets in an Ahlfors
be a sequence of open sets in an Ahlfors ![]() -regular metric space
-regular metric space ![]() , and let
, and let ![]() be a dimension function such that
be a dimension function such that
(1) 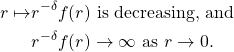
Fix ![]() , and suppose that the following hypothesis holds:
, and suppose that the following hypothesis holds:
\begin{itemize}
\item[(*)] For every ball ![]() and for every
and for every ![]() , there exists a probability measure
, there exists a probability measure ![]() with
with ![]() , such that for every ball
, such that for every ball ![]() , we have
, we have
(2) 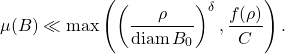
\end{itemize}
Then for every ball ![]() ,
,
![]()
In particular, if the hypothesis \text{(*)} holds for all ![]() , then
, then
![]()
\end{theorem}
The condition \eqref{f2} is a natural condition which implies that ![]() . A consequence of this theorem is the celebrated Mass Transference Principle of Beresnevich-Velani (2006).
. A consequence of this theorem is the celebrated Mass Transference Principle of Beresnevich-Velani (2006).
