I have experience teaching within Australia and abroad (England and Pakistan). I have experience observing teaching practices in America (Brandeis University) and Denmark (Aarhus University) and have been teaching since 2004. My teaching experiences have impacted my teaching philosophy and practices and will continue to shape me as an educator.
Please send me an email for a Teaching Portfolio including my teaching philosophy.
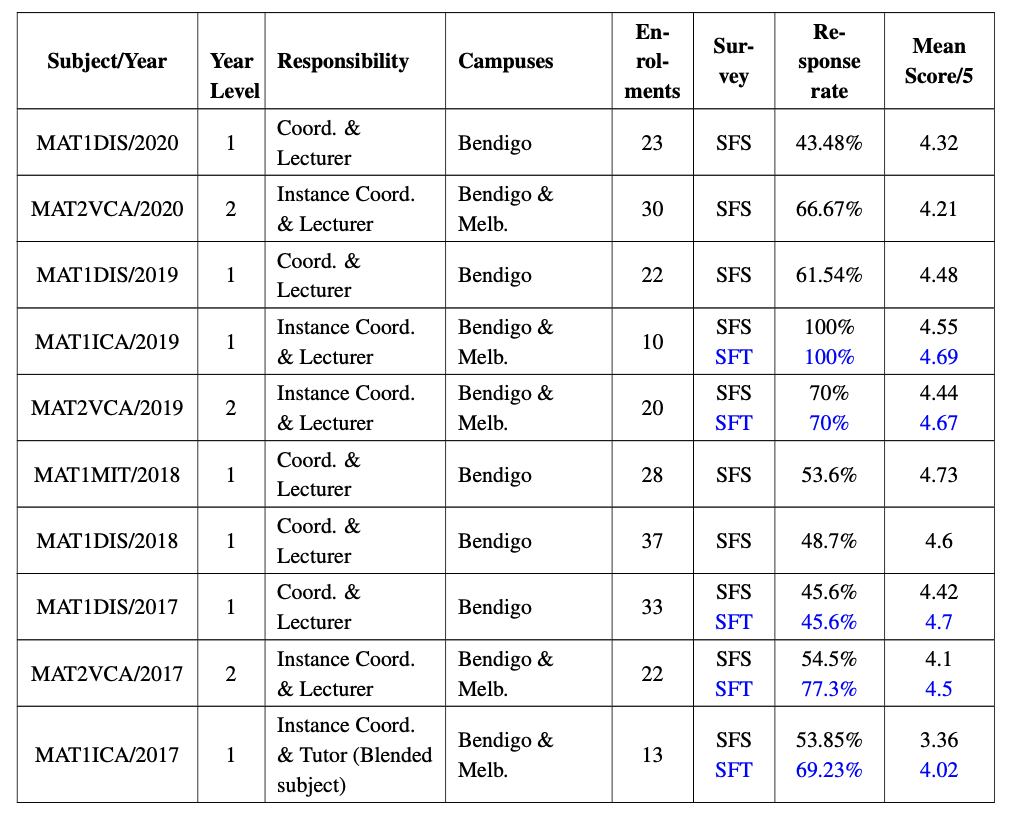
Student Evaluations (La Trobe University)
The formal online SFS surveys were conducted for subjects I lectured or coordinated. I requested student feedback on teaching which gives additional feedback on my teaching style and practices. My quantitative scores are listed below.
The University of Newcastle
The formal online SFS surveys were conducted for courses I lectured or coordinated. My quantitative scores were above the university (and school) averages and higher than previous offerings.

Teaching Awards and Research Projects
Teaching Awards
In recognition of my contributions to students learning I was awarded the 2016 UoN Faculty of Science Teaching Award (Individual) and received a high commendation for Team Teaching.

Teacher of the Year 2016 The University of Newcastle
Teacher of the Year 2016 The University of Newcastle

High commendation for Team Teaching 2016
Research Projects (Teaching)
I have been involved in teaching related research projects funded by The Centre for Equity and Equality in Higher Education (CEEHE) at UoN.
-
- The project “Enabling pedagogies and transitions: a community of practice across pre-undergraduate and undergraduate mathematics at The University of Newcastle” aimed to better understand and build relationships between mathematical educators. This project investigated links between mathematical educators across a variety of disciplines ($9217).
- The project “Is a BMath/STEM degree for a privileged few”. It was aimed at supporting diverse students to better understand aspirations/concerns of student undertaking mathematical study ($15000).
These projects were commissioned to support diversity by building a stronger community between mathematical educators from multiple disciplines, allowing for a dialogue to commence which reflects on others success in teaching.


